Brunskill - Lecture 1

lecture Link

A high-level Overview

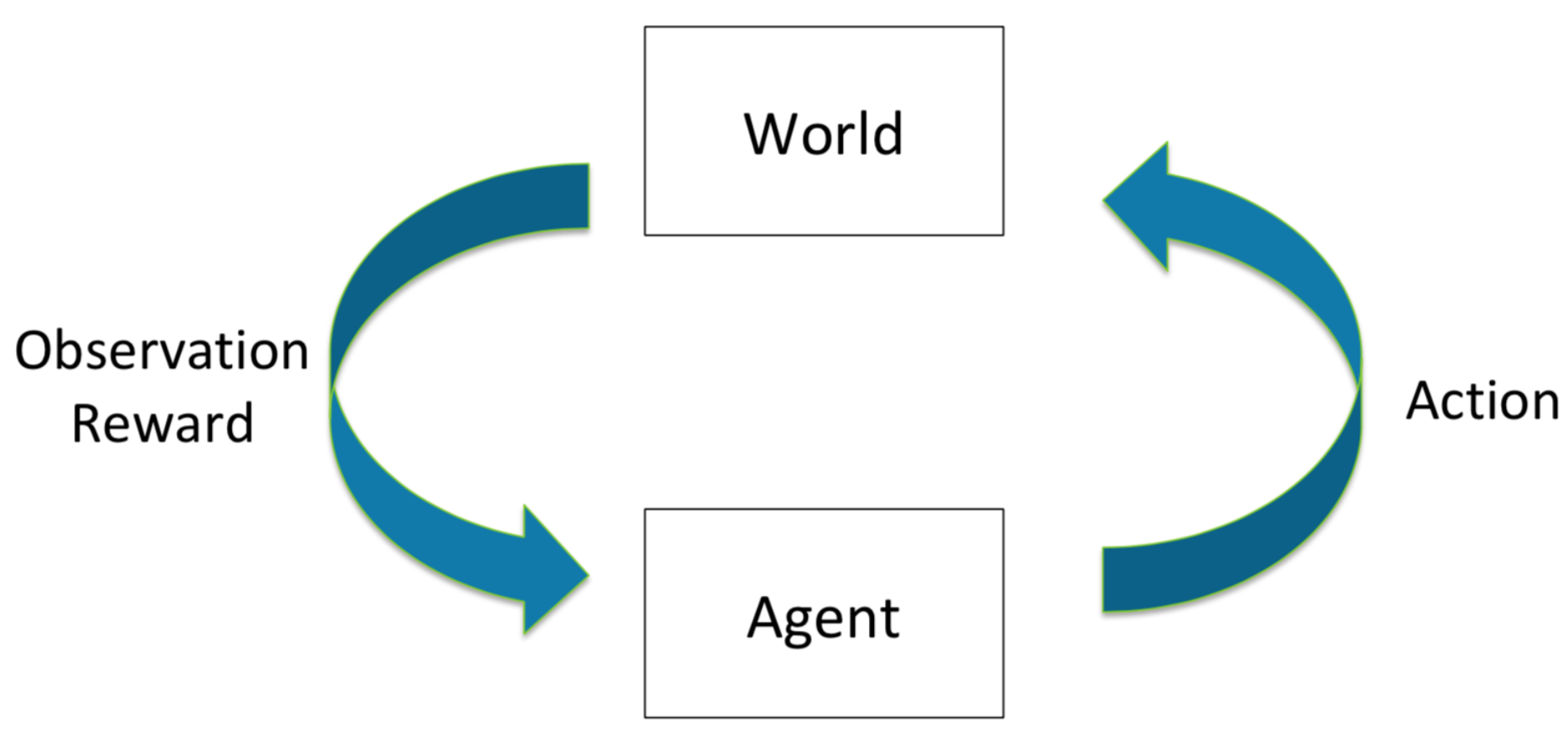Source: Class lecture note.

Examples

1. In the case of auction design, an agent can be the mechanism designer. An action is the choice of a particular mechanism. The world consists of a list of participants, their types, and a collection of possible outcome. Then the reward can be the resulting social welfare or the revenue.

2. In (auto) bidding, it is reversed. An agent is an advertiser. The world is the underlying mechanism, and possibly other advertisers. An action is a bidding strategy, and the outcome is the utility (ROI, number-of-conversions, ect.) for which this advertiser obtains.

Each (discrete) time step $t$:

1. The agent makes a decision (an action) based on the history (a collection of previous actions taken, observations of the world, and rewards, if such information exists).

2. The world updates based on the decision.

3. The world outputs a reward and an observation to the agent.

Markov assumption

The new state of the world can only depends on the current state and the current action taken, without needing to look at the sequence of past states and actions. Under this Markov assumption, when making a decision, an agent only need to consider the current state.

Two models in a RL system

1. Dynamics model: predicts the next state, $P(s_{t+1} = s' | s_t = s, a_t = a)$.

2. Reward model: predicts the immediate reward, $r(s_t = s, a_t = a) = \mathbb{E}[r_t | s_t = s, a_t = a]$.

A policy

A function an agent uses to maps states to actions. Could be either deterministic or stochastic.

Markov Reward Process (MRP)

A Markov chain + rewards

1. A set $S$ of states.

2. A transition model $P(s' | s)$

3. A reward model $R(s) = \mathbb{E}[r_t | s_t = s]$.

4. A discount factor $\gamma \in [0, 1]$.

No actions in a MRP

Horizon $H$

Defined as the number of time steps in each episode. Can be infinite.

Return $G_t$ for a Markov reward process

A random variable representing the discounted sum of rewards from time $t$ to the end of an episode. Defined as $G_t = r_t + \gamma r_{t+1} + ... + \gamma^{H-1} r_{t + H - 1}$. Note that the return is defined w.r.t. a time step, not a state.

The state value function $V(s)$

The expected return from starting in a state $s$, $V(s) = \mathbb{E}[G_t | s_t = s]$. Note that the value function is defined w.r.t. a state, not a time step.

Where does the randomness come from

So far, it seems that there are three possible sources:

1. The environment (often assumed to be Markov)

2. The policy, if stochastic

3. The reward function itself can also be randomized

What does a learning agent know in general

1. The current observed state, which may or may not fully describe the current environment. Also the history of observed states.

2. The immediate reward value.

3. What actions the agent can take (the action space).

Generally does not know the followings:

1. How the environment works (e.g., the transition matrix).

2. The reward function.

3. An optimal policy.